34) What is the time complexity T(n) of the nested loops below? For simplicity, you may assume that n is a power of 2. That is, n = 2k for some positive integer k.

외반복문은 n회만, 내반복문은 2^n회만 반복된다.
중첩 반복문의 시간 복잡성은 곱으로 표현되므로,
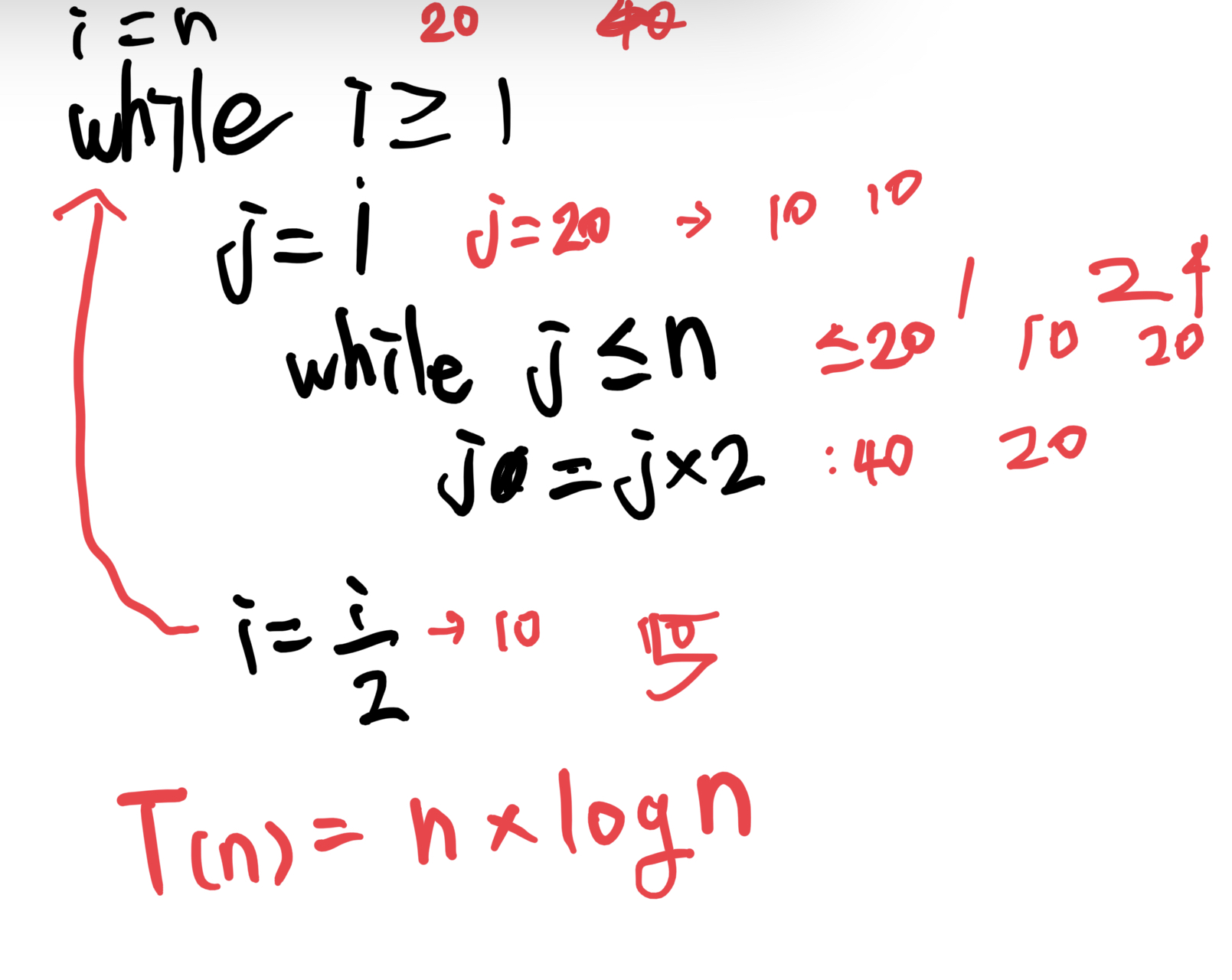
맨 아래처럼 빨간 글자로 구원받는다.
(n을 넣으면 2의 n회 반복되므로 복잡도는 지수의 역인 로그가 된다)
정렬 알고리즘
1) 병합 정렬
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include<iostream>
using 네임스페이스 std;
int N, arr(1000001);
int* arr2;
void merge (int left, int 오른쪽)
{
int mid = (왼쪽 + 오른쪽) / 2;
int i = left;
int j = mid + 1;
int k = left;
while (i <= mid && j <= 오른쪽)
{
if (arr(i) <= arr(j))
arr2(k++) = arr (i++);
else
arr2(k++) = arr (j++);
}
int tmp = i > mid/j:i;
while (k <= right) arr2(k++) = arr (tmp++);
for (int i = left; i <= right; i++) arr(i) = arr2(i);
}
void partition (int left, int 오른쪽)
{
int mid;
if (왼쪽 < 오른쪽)
{
mid = (왼쪽 + 오른쪽) / 2;
partition(left, mid);
partition (mid + 1right);
merge (left, right);
}
}
int main()
{
cin>>N;
arr2 = 새로운 int(N);// 생일을 0310 이렇게 숫자로 받기
for (int i = 0;i < N; i++) scanf(“%d”, &arr(i));
partition (0N – 1);
for (int i = 0;i < N; i++) printf(“%d\n”arr(i));
}
|
cs |
시간의 복잡성:
병합 알고리즘은 숫자 다이어그램과 같이 N이 클수록 사례가 나뉘기 때문에 제곱으로 늘어나기 때문에 시간 복잡성은
n의 제곱에 따라
2) 삽입 정렬
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#include<iostream>
using 네임스페이스 std;
void insertion_sort (int arr())
{
int 키, j, i;
for (i = 1;i < 10;i++) { // 1
키 = arr(i);
for (j = i – 1;j >= 0 && arr(j) > 키; j––) { //2
arr (j + 1) = arr(j);
}
arr (j + 1) = 키; //3
}
}
int main()
{
int N;
cin >> N;
int* arr = 새로운 int(N);
for (int i = 0;i < 10;i++) {
cout << arr(i) << ” “;
}
insertion_sort(arr);
return 0;
}
|
cs |
삽입 정렬은 최악의 경우 중첩 된 반복 문에서 모든 키가 올바른 위치로 돌아가는 것을 반복해야합니다.
n번의 반복문이 중첩된다.
따라서 시간의 복잡성은 n^2로 표현할 수 있다.
3) 선택 정렬
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
#include<iostream>
using 네임스페이스 std;
void Swap (int& a, int& b) {
int tmp;
tmp = a;
a = b;
b = tmp;
}
void SelectionSort (int* arr, int len) {
int min_idx;
for (int i = 0;i < len – 1;i++) {
min_idx = i;
for (int j = i + 1;j < len; j++) {
if (arr(min_idx) > arr(j)) {
min_idx = j;
}
}
Swap(arr(min_idx), arr(i));
}
}
int main(void) {
int n;
cin >> n;
int* arr = 새로운 int(n);
for (int i = 0;i < n; i++) {
cout << arr(i) << ” “;
}
cout << endl;
SelectionSort(arr, n);
for (int i = 0;i < n; i++) {
cout << arr(i) << ” “;
}
return 0;
}
|
cs |
선택 소트는 최저치를 요구해 맨 앞에 하나씩 두도록 하므로, n개의 숫자가 있으면 1부터 n-1회 반복을 시행한다
따라서, 1+2+…+n-1=(1+(n-1))(n-1)/2의 복잡도를 따르게 되므로, 가장 효율이 좋다.