(프로그래머스/LV4) 미로 탈출 (Python)

  • by

Problem: https://school.programmers.co.kr/learn/courses/30/lessons/81304

프로그래머스

코드 중심 개발자 채용. 스택 기반 포지션 매칭 프로그래머스 개발자를 위한 커스텀 프로파일을 등록하고 나와 기술의 궁합이 잘 맞는 기업을 매칭합니다.

programmers.co.kr

인기글

Status: Solve

시간: 00:34:34

문제 설명

더 보기

신규 게임 「카카오 미로 탈출」이 릴리스되어, 라이언이 베타 테스터로 참가했습니다.


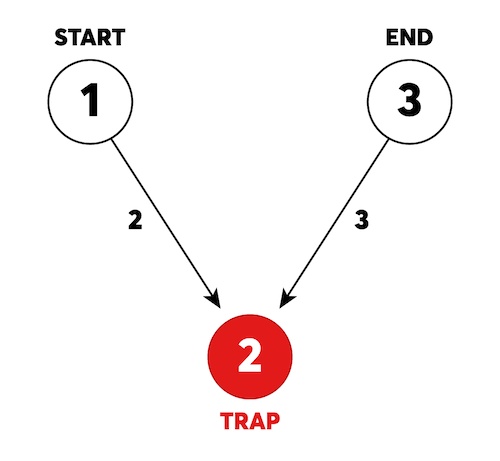
위의 그림은 카카오 미로 탈출의 초기 상태를 보여줍니다.

1번에서 3번까지 번호가 붙은 3개의 방이 있으며, 방과 방 사이를 연결하는 길에는 이동에 걸리는 시간이 표시되어 있습니다.

도로는 화살표가 가리키는 방향으로만 이동할 수 있습니다.

미로에는 트랩이 존재하고 트랩으로 이동하면 이동한 트랩과 관련된 모든 화살표의 방향이 변경됩니다.


출발지인 1번 방에서 탈출이 가능한 3번 방까지 이동할 필요가 있습니다.

도망치는 데 필요한 최단 시간을 찾습니다.

  • 도면 중의 원은 방을 나타내고, 원 안의 숫자는 방 번호를 나타낸다.
    • 방이 n개인 경우 방 번호는 1에서 n까지 사용됩니다.

  • 화살표에 표시된 숫자는 방과 방 사이를 이동하는 데 걸리는 시간을 나타냅니다.
    • 화살표가 가리키는 방향으로만 이동이 가능합니다.

      즉, 위의 그림에서는 2개 방에서 1개 방으로 이동할 수 없습니다.

  • 그림에 표시된 빨간 방인 2번 방은 함정입니다.
    • 함정 방으로 이동하는 순간, 이동한 함정 방과 연결된 모든 길의 방향이 반대가 됩니다.

    • 위 그림 1번 방에서 2번 방으로 이동하는 순간 1에서 2로 이동할 수 있는 길은 2에서 1로 이동할 수 있는 길로 바뀌고, 3에서 2로 이동할 수 있는 길은 2에서 3으로 이동할 수 있는 길로 바뀝니다.

    • 같은 함정 방을 두 번째로 방문하면 원래 방향의 길로 돌아갑니다.

      즉, 여러 번 방문할 수 있습니다.

  • 미로를 탈출하는 데 필요한 최소 시간은 다음과 같습니다.
    • 1→2：2번 방으로 이동합니다.

      이동 시간은 2입니다.

    • 트랩 발동: 2번 방으로 이어지는 모든 길의 방향이 반대가 됩니다.

    • 2→3：3번 방으로 이동합니다.

      이동 시간은 3입니다.

    • 탈출에 성공했습니다.

      총 이동 시간은 5입니다.

방 수를 나타내는 정수 n, 출발 방 번호 start, 도착 방 번호 end, 통로와 이동 시간을 나타내는 2 차원 정수 배열 roads, 함정 방 번호를 포함하는 정수 배열 traps가 매개 변수로 주어지면 미로 탈출하는 데 필요한 최소 시간을 반환하려면 솔루션 함수를 완성하십시오.

입출력

더 보기

제한사항

  • 2 ≤ n ≤1,000
  • 1≤ 시작 ≤ n
  • 1≤ 끝 ≤ n
  • 1≤ 로드의 행 길이 ≤3,000
  • 도로의 행은 (P, Q, S)로 구성됩니다.

    • P에서 Q로 갈 수 있는 길이 있고 길을 따라 이동하는데 S만큼 시간이 걸립니다.

    • 1≤ P ≤ n
    • 1≤ Q ≤ n
    • P ≠ Q
    • 1≤ S ≤3,000
    • 두 개의 서로 다른 방 사이에 직접 연결된 길이가 여러 개있을 수 있습니다.

  • 0 ≤ 트랩 길이 ≤10
    • 1≤ traps의 원소≤ n
    • 출발실과 도착실은 함정이 아닙니다.

  • 항상 미로를 탈출할 수 있는 경우에만 주어집니다.

입출력 예

n 시작 끝 nodes traps 결과
3 1 3 ((1, 2, 2), (3, 2, 3)) (2) 5
4 1 4 ((1, 2, 1), (3, 2, 1), (2, 4, 1)) (2, 3) 4

풀

처음에는 트랩의 최대 길이를 n으로 잘못보고 매우 기뻤습니다 …

기본적으로 최소 길이 네비게이션이므로 힙을 사용하여 다이스트라 알고리즘를 이용한다.

트랩의 최대 길이는 10이므로 트랩 방문을 저장합니다.

비트 마스킹를 이용하면 된다.

각 트랩 번호의 색인을 저장하고, 색인 방문 여부를 1과 0으로 구분합니다.

1은 그 트랩을 홀수회 방문했다는 의미이고, 0은 짝수회를 방문했다는 의미이다.

  • edge 정보를 저장할 때 발신 아웃 코스와 들어오는 인코스를 저장합니다.

    엔코스는 (Q, P, S) 순서로 저장하면 간단합니다.

  • 함정방 방문 정보가 중요한 이유: 아웃코스와 인코스를 구별하기 위해서다.

    함정 방에 방문하면 가장자리의 방향이 바뀌므로(즉, 그 노드에 인접한 인코스와 아웃 코스 정보가 반대가 되기 때문에), 각 함정 방을 홀수회, 혹은 짝수회 방문했는지 여부가 중요하기 때문이다 .
  • 다음과 같은 상황이 있을 수 있습니다.

    • 일반 노드 -> 일반 노드 : 일반적인 경우이므로, 아웃 코스만을 고려하면 된다.

    • 일반 노드 -> 트랩 노드 / 트랩 노드 -> 트랩 노드 / 트랩 노드 -> 일반 노드 : 사실상 이 경우를 고려하기 위해 비트 마스킹을 고려하게 된다.

      각 트랩 노드를 방문한 총합이 홀수번인지 짝수번인지에 따라 엣지 방향이 결정되기 때문이다.

      합이 짝수번인 경우 방향은 유지됩니다.

      (즉, 아웃 코스를 사용하는) 홀수 번호라면 방향은 유지되지 않습니다.

      (인코스 이용)
  • 또한 방문의 총 수를 저장하는 것은 매우 비효율적입니다.

    따라서 홀수 번 방문할지 여부를 저장하지만 인덱스의 XOR 연산을 사용할 수 있습니다.

    홀수 및 짝수 연산 결과의 진리표는 XOR 연산의 진리표와 동일하기 때문에. 일반 노드는 방문하지 않은 (제로 값) 트랩 노드로 간주될 수 있습니다.

    아웃 코스의 가장자리에 대해 두 개의 노드를 방문하지 않았거나 두 개의 노드를 방문한 경우 해당 가장자리를 사용할 수 있습니다.

    . 인코스의 에지에 대해서는, 나머지의 경우(한 함정 노드만 방문했을 때)에 한해, 그 엣지를 이용할 수 있다.

  • 함정 방을 방문하는 경우, 그 함정 색인에 대해 XOR 연산을 취함으로써 함정의 방문 여부를 갱신할 수 있다.

풀 코드

from collections import defaultdict
from heapq import heappush, heappop
MAX = float('inf')

def solution(n, start, end, roads, traps):
    in_road_dict = defaultdict(list)
    out_road_dict = defaultdict(list)
    max_traps = len(traps)
    
    is_trapped = lambda x, trapped : x in traps and trapped | 1 << traps.index(x) == trapped
    visited = ((MAX)*(1 << max_traps) for _ in range(n+1))
    visited(start)(0) = 0
    
    for P, Q, S in roads :
        out_road_dict(P).append((Q, S))
        in_road_dict(Q).append((P, S))
        
    answer = MAX
    
    q = ((0, 0, start))
    
    while q :
        dist, trapped, node = heappop(q)
        if node == end :
            return dist
        
        is_cur_trapped = is_trapped(node, trapped)
        
        for next_node, next_dist in in_road_dict(node) :
            is_next_trapped = is_trapped(next_node, trapped)
            if is_cur_trapped ^ is_next_trapped :
                next_trapped = trapped ^ (1 << traps.index(next_node)) if next_node in traps else trapped
                if visited(next_node)(next_trapped) > dist + next_dist :
                    visited(next_node)(next_trapped) = dist + next_dist
                    heappush(q, (dist + next_dist, next_trapped, next_node))
                
        for next_node, next_dist in out_road_dict(node) :
            is_next_trapped = is_trapped(next_node, trapped)
            if not is_cur_trapped ^ is_next_trapped :
                next_trapped = trapped ^ (1 << traps.index(next_node)) if next_node in traps else trapped
                if visited(next_node)(next_trapped) > dist + next_dist :
                    visited(next_node)(next_trapped) = dist + next_dist
                    heappush(q, (dist + next_dist, next_trapped, next_node))

    return 0


수영장이 완성!