Read Chapter 8.
1. Prove that the smallest height for any tree on n nodes is Ω(lg n) = – 1 + lg(n+1).
하한은 높이 h의 완전한 바이너리 트리를 조사하여 증명할 수 있습니다.
완전한 바이너리 트리? 높이가 k이면 레벨 1에서 k-1까지 노드가 모두 채워집니다.
(=리프 노드대신 모든 노드에는 두 개의 자식이 있습니다.
)
-> 추가 노드를 잎 노드에 연결하면? 높이도 증가했습니다.
동일한 수의 노드를 가진 바이너리 트리의 최소 높이가 있습니다!
| 깊이(h), 노드 수(n) h = 0, 최대 n = 1 h=1, 최대 n=2 h=2, 최대 n=4 … -> 트리 깊이가 h이면 노드 수는 2^h개 n<=1+2+2^2+....2^h |
1 + 2 + 2^2 + …. 2^h = 2^(h+1) – 1 ( : 깊이 h 의 전체 바이너리 트리에 n 개의 노드가 있음)
(그럼 어떻게 1 + 2 + 2^2 + …. 2^h = 2^(h+1) – 1이 될 것인가? )
**시그마로 등식 표기: (k=0에서 h까지, 2^n+1 표기와 동일)
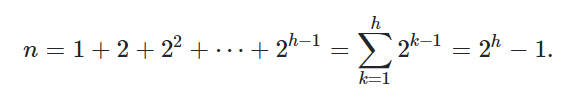
| – 귀납 기초 : d=0, 2^0 = 1 = 2^(0+1) – 1 – 귀납 과정 : 임의의 음이 아닌 정수 d에 대해 다음 식이 성립한다고 가정 -> 2^0 +2^1 + 2^2 + …. 2^d = 2^(d+1) – 1 – 귀납 단계: 2^0 + 2^1 + 2^2 + …. 2^(d+1) = 2^((d+1)+1) – 1 -> 성립하시겠습니까? 2^0 + 2^1 + 2^2 + …. 2^(d+1) = 2^0 +2^1 +2^2 +….2^d + 2^(d+1) = 2^(d+1) – 1 + 2^(d+1) = 2* 2^(d+1) – 1 = 2^((d+1)+1) -1 |
==> 이렇게, n<= 2^(h+1) – 1
n 2^(h+1)
lg n < h + 1
lg n <= h
n<= 2^(h+1) -1
lg n <= h + 1 - lg
lg (n+1) -1 <= h
==>Ω(lg n) = lg(n+1) -1
Proving that a Binary Tree of $n$ nodes has a height of at least $\log(n)$.
For a homework assignment, I need to prove that a Binary Tree of $n$ nodes has a height of at least $log(k)$. I started out by testing some trees that were filled at every layer, and checking $log( …
math.stackexchange.com
The height of any binary tree of n nodes is between log(n) and n-1. What is the proof for this observation?
Answer (1 of 5): Suppose a binary tree has n nodes. There’s at most 1 node (the root) at height 0, at most 2 nodes (2 children of the root) at height 1, at most 4 nodes (2 children each for the 2 children of the root) at height 2, and so on. So, for a tree
www.quora.com
2. When you shrink the space of direct access arrays, you might want to use a linked list data structure. What would be the problem if you use the linked list? Show your answer with explaining the time complexity.
-> what is the linked list ? ; 각 노드가 데이터와 포인터를 가지고 한 줄에 연결되고 데이터를 저장하는 데이터 구조
액세스 시간의 복잡성: O(n)
- 인덱스 x의 노드에 액세스하는 방법?헤드에서 다음 노드로 x 번 이동
- 마지막 노드에 액세스하는 방법?헤드에서 마지막 노드까지 n-1번 가야 합니다.
- 최악의 경우의 시간 복잡도: O(n)
네비게이션 시간의 복잡성: O(n)
- 헤드 노드에서 다음 노드를 하나씩 보면서 원하는 데이터가 있는 노드를 찾습니다.
(배열을 탐색할 때와 같은 방법, 선형 탐색을 이용) - 연결 목록에 검색할 데이터가 없거나 검색할 데이터가 마지막 노드에 있는 경우. n개의 노드를 모두 보아야 합니다.
- 최악의 경우의 시간 복잡도: O(n)
삽입 / 삭제 (Insertion / Deletion) 시간 복잡성 : O (1)
- 삽입, 삭제하는 노드의 주변 노드의 링크만을 수정하면 된다.
- 따라서 삽입, 삭제가 수행되는 시간은 특정 값에 비례하지 않고 항상 일정합니다.
- 시간 복잡도: O(1)
==>삽입, 삭제 조작에는 네비게이션 조작이 필요합니다!
(어떤 노드를 삭제, 삽입할 것인가..)
즉, 결국 삽입, 삭제 조작 자체는 O(1)의 시간 복잡도를 가지지만, 탐색 연산 때문에 최악의 경우 O(n)의 시간 복잡도가 필요하다는 문제가 발생한다.
(Data Structure) 연결 목록
링크 목록이란 무엇입니까? 연결 리스트(Linked List)는 각 노드가 데이터와 포인터를 가지고 일행으로 연결되는 방식으로 데이터를 저장하는 데이터 구조이다.
데이터가 포함된 노드 연결
hyeinisfree.
(자료 구조) 싱글 링크드 리스트(단순 접속 리스트)의 시간 복잡도
단일 링크 목록(단순 연결 목록) 작업의 시간 복잡성을 살펴보겠습니다.
액세스 시간 복잡성 인덱스 x의 노드에 액세스하려면 head에서 다음 노드로 x 번 앞으로 이동
codingstudyroom.
3. In the hash family function, a should not equal to 0. Why? Please give me a simple answer (one sentence).
4. Use the birthday dataset, Do the followings:
4.1. Put them into your unordered array using set.
4.2. Put them into the sorted array set.
4.3. Put them into the direct access array set
4.4. Put them into the hash table set.
4.5. Compare their size.
4.6. Compare their interfaces: build, find, insert, delete, find_min, find_max, find_next, find_prev.